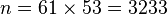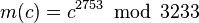Chinese Remainder Theorem - Program in C

#include<stdio.h>
#include<stdlib.h>
long long int modularMultiplicativeInverse_BruteForce(long long int e,long long int mod)
{
    long long int i;
    for(i=1;i<mod;i++)
        if((e*i)%mod==1)
            return i;
}
int main()
{
    long long int i,n,*a,*b,*m,M,*Marray,answer;
    printf("Enter the number of Equations : \n");
    scanf("%lld",&n);
    a=(long long int*)malloc(sizeof(long long int)*n);
    m=(long long int*)malloc(sizeof(long long int)*n);
    Marray=(long long int*)malloc(sizeof(long long int)*n);
    printf("Enter the array a :\n");
    for(i=0;i<n;i++)
        scanf("%lld",&a[i]);
    printf("Enter the array m (all the elements of m should be pairwise co-prime) :\n");
    for(i=0;i<n;i++)
        scanf("%lld",&m[i]);
    M=1;
    for(i=0;i<n;i++)
        M*=m[i];
    for(i=0;i<n;i++)
        Marray[i]=M/m[i];
    answer=0;
    for(i=0;i<n;i++)
        answer = (answer + ((a[i] * Marray[i])%M * modularMultiplicativeInverse_BruteForce(Marray[i],m[i]))%M)%M;
    printf("x = %lld\n",answer);
    return 0;
}

Euclidean Algorithm for finding GCD of two numbers - Program in C

#include<stdio.h>

long long int gcd_Euclid_Recursive(long long int a,long long int b)
{
    if(b==0)
        return a;
    return gcd_Euclid_Recursive(b,a%b);
}


long long int gcd_Euclid_NonRecursive(long long int a,long long int b)
{
    long long int r;
    while(b!=0)
    {
        r=a%b;
        a=b;
        b=r;
    }
    return a;
}

int main()
{
    long long int a,b;
    printf("Enter two number : ");
    scanf("%lld%lld",&a,&b);
    printf("gcd(%lld,%lld) = %lld\n",a,b,gcd_Euclid_Recursive(a,b));
    printf("gcd(%lld,%lld) = %lld\n",a,b,gcd_Euclid_NonRecursive(a,b));
    return 0;
}

Rail Fence Cipher - Program in C

In the rail fence cipher, the plaintext is written downwards and diagonally on successive "rails" of an imaginary fence, then moving up when we reach the bottom rail. When we reach the top rail, the message is written downwards again until the whole plaintext is written out. The message is then read off in rows. For example, if we have 3 "rails" and a message of 'WE ARE DISCOVERED. FLEE AT ONCE', the cipherer writes out:

W . . . E . . . C . . . R . . . L . . . T . . . E
. E . R . D . S . O . E . E . F . E . A . O . C .
. . A . . . I . . . V . . . D . . . E . . . N . .

Then reads off to get the ciphertext:

WECRL TEERD SOEEF EAOCA IVDEN

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
char *plainTextToCipherText(char plainText[],int n)
{
    int i,j,counter,limit,index=0,len;
    char *cipherText;
    len=strlen(plainText);
    cipherText=(char*)malloc(sizeof(char)*(len+1));
    for(i=0;i<n;i++)
 {
  counter=0;
  for(j=i;j<len;j+=limit)
  {
   cipherText[index++]=plainText[j];
   if(i==0 || i==n-1)
       limit=2*n-2;
   else if(counter%2==0)
    limit=2*(n-i-1);
   else
    limit=2*i;
   if(limit<=0)
       break;
   counter++;
  }
 }
 cipherText[index]='\0';
 return cipherText;
}
int main()
{
 int n;
 char plainText[100];
 printf("Enter the plain text : ");
 scanf("%s",plainText);
 printf("Enter the value of n : ");
 scanf("%d",&n);
    printf("%s\n",plainTextToCipherText(plainText,n)); 
 return 0;
}

RSA Algorithm - Program in C

RSA is one of the first practical public-key cryptosystems and is widely used for secure data transmission. In such a cryptosystem, theencryption key is public and differs from the decryption key which is kept secret. In RSA, this asymmetry is based on the practical difficulty of factoring the product of two large prime numbers, the factoring problem. RSA is made of the initial letters of the surnames ofRon Rivest, Adi Shamir and Leonard Adleman, who first publicly described the algorithm in 1977. 

The RSA algorithm involves three steps: key generation, encryption and decryption.

Key generation

RSA involves a public key and a private key. The public key can be known by everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted in a reasonable amount of time using the private key. The keys for the RSA algorithm are generated the following way:

1. Choose two distinct prime numbers p and q.
   • For security purposes, the integers p and q should be chosen at random, and should be of similar bit-length. Prime integers can be efficiently found using a primality test.
2. Compute n = pq.
   • n is used as the modulus for both the public and private keys. Its length, usually expressed in bits, is the key length.
3. Compute φ(n) = φ(p)φ(q) = (p − 1)(q − 1) = n - (p + q -1), where φ is Euler's totient function. This value is kept private.
4. Choose an integer e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1; i.e., e and φ(n) are coprime.
   • e is released as the public key exponent.
   • e having a short bit-length and small Hamming weight results in more efficient encryption – most commonly 2¹⁶ + 1 = 65,537. However, much smaller values of e (such as 3) have been shown to be less secure in some settings.^[5]
5. Determine d as d ≡ e⁻¹ (mod φ(n)); i.e., d is the modular multiplicative inverse of e (modulo φ(n)).

• This is more clearly stated as: solve for d given d⋅e ≡ 1 (mod φ(n))
• This is often computed using the extended Euclidean algorithm. Using the pseudocode in the Modular integers section, inputs a and n correspond to e and φ(n), respectively.
• d is kept as the private key exponent.

The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d, which must be kept secret. p, q, and φ(n) must also be kept secret because they can be used to calculate d.

Encryption

Alice transmits her public key (n, e) to Bob and keeps the private key d secret. Bob then wishes to send message M to Alice.

He first turns M into an integer m, such that 0 ≤ m < n by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext c corresponding to

This can be done efficiently, even for 500-bit numbers, using Modular exponentiation. Bob then transmits c to Alice.

Note that at least nine values of m will yield a ciphertext c equal to m,^{[note 1]}

Decryption[edit]

Alice can recover m from c by using her private key exponent d via computing

Given m, she can recover the original message M by reversing the padding scheme.

(In practice, there are more efficient methods of calculating c^d using the precomputed values below.)

A worked example[edit]

Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.

1. Choose two distinct prime numbers, such as

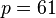    and 

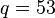
2. Compute n = pq giving

   

3. Compute the totient of the product as φ(n) = (p − 1)(q − 1) giving

   

4. Choose any number 1 < e < 3120 that is coprime to 3120. Choosing a prime number for e leaves us only to check that e is not a divisor of 3120.

   Let 

5. Compute d, the modular multiplicative inverse of e (mod φ(n)) yielding,

   

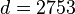
   Worked example for the modular multiplicative inverse:

   

   

The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is

The private key is (d = 2753). For an encrypted ciphertext c, the decryption function is

For instance, in order to encrypt m = 65, we calculate

To decrypt c = 2790, we calculate

Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real-life situations the primes selected would be much larger; in our example it would be trivial to factor n, 3233 (obtained from the freely available public key) back to the primes p and q. Given e, also from the public key, we could then compute d and so acquire the private key.

/*
    Sample test case 1 :
        Choose p = 3 and q = 11
        Compute n = p * q = 3 * 11 = 33
        Compute φ(n) = (p - 1) * (q - 1) = 2 * 10 = 20
        Choose e such that 1 < e < φ(n) and e and n are coprime. Let e = 7
        Compute a value for d such that (d * e) % φ(n) = 1. One solution is d = 3 [(3 * 7) % 20 = 1]
        Public key is (e, n) => (7, 33)
        Private key is (d, n) => (3, 33)
        The encryption of m = 2 is c = 27 % 33 = 29
        The decryption of c = 29 is m = 293 % 33 = 2
        
    Sample test case 2 :
        Choose p = 61 and q = 53
        Compute n = p * q = 61 * 53 = 3233
        Compute φ(n) = (p - 1) * (q - 1) = 60 * 52 = 3120
        Choose e such that 1 < e < φ(n) and e and n are coprime. Let e = 17
        Compute a value for d such that (d * e) % φ(n) = 1. One solution is d = 2753 [(2753 * 17) % 20 = 1]
        Public key is (e, n) => (17, 3233)
        Private key is (d, n) => (2753, 3233)
        The encryption of m = 65 is c = 2790
        The decryption of c = 2790 is m = 65
*/
#include<stdio.h>
/*
    Exponentiation by squaring
        http://en.wikipedia.org/wiki/Exponentiation_by_squaring
*/
long long int power(long long int a,long long int b,long long int mod)
{
    long long int t;
    if(b==0)
        return 1;
    else if(b==1)
        return a;
    t=power(a,b/2,mod);
    if(b%2==0)
        return (t*t)%mod;
    else
        return (((t*t)%mod)*a)%mod;
}

/*
    Euler's theorem may be used to compute modular inverse:
    According to Euler's theorem, if a is coprime to m, that is, gcd(a, m) = 1, then
        
        inverse of a = power(a,m-2) % m 
        
    but for Euler's m must be prime.
        and our mod will never be prime.
            because mod is phi(n) = (p-1)*(q-1) ... so this is never prime.
    so we cant apply Eulers Theorem to find multiplicative inverse of e
*/
/*
long long int modularMultiplicativeInverse_Euler(long long int e,long long int mod)
{
    return power(e,mod-2,mod);
}
*/
/*
long long int modularMultiplicativeInverse_ExtendedEuclideantheorem(long long int e,long long int mod)
{
    
}
*/
long long int modularMultiplicativeInverse_BruteForce(long long int e,long long int mod)
{
    long long int i;
    for(i=1;i<mod;i++)
        if((e*i)%mod==1)
            return i;
}
long long int encrypt(long long int m,long long int e,long long int n)
{
    return power(m,e,n);
}
long long int decrypt(long long int c,long long int d,long long int n)
{
    return power(c,d,n);
}
int main()
{
 long long int p,q,n,phin,d,e,m,c;
 // p and q should be prime numbers of similar bit length.
 printf("Enter the value of p and q (p and q should be primes of similar bit length) :\n");
 scanf("%lld%lld",&p,&q);
 n=p*q;
 phin=(p-1)*(q-1);

 printf("Enter an integer e such that 1 < e < %lld, and gcd(e,%lld)=1 : ",phin,phin);
 scanf("%lld",&e);

 printf("NOTE : %lld,%lld is your public key.\n",e,n);
 // e is called the public key exponent
 
 d=modularMultiplicativeInverse_BruteForce(e,phin);
 printf("NOTE : %lld,%lld is your private key.\n",d,n);
 // d is called the private key exponent
    
    printf("\nEnter the number to be encrypted : ");
    scanf("%lld",&m);
    c=encrypt(m,e,n); // sending the message to be encrypted and the public key.
    printf("the encrypted message is : %lld\n",c);
    
    printf("\nEnter the number to be decrypted : ");
    scanf("%lld",&c);
    m=decrypt(c,d,n); // sending the cipher message to be decrypted and the private key.
    printf("the decrypted message is : %lld\n",m);
 return 0;
}

Diffie Hellman Key Exchange Algorithm - Program in C

Diffie–Hellman establishes a shared secret that can be used for secret communications while exchanging data over a public network. The crucial part of the process is that Alice and Bob exchange their secret colors in a mix only. Finally this generates an identical key that is computationally difficult (impossible for modern supercomputers to do in a reasonable amount of time) to reverse for another party that might have been listening in on them. Alice and Bob now use this common secret to encrypt and decrypt their sent and received data. 

The simplest and the original implementation of the protocol uses the multiplicative group of integers modulo p, where p is prime, and g is a primitive root modulo p. Here is an example of the protocol, with non-secret values in blue, and secret values in red.

1. Alice and Bob agree to use a prime number p = 23 and base g = 5 (which is a primitive root modulo 23).
2. Alice chooses a secret integer a = 6, then sends Bob A = g^a mod p
   • A = 5⁶ mod 23 = 8
3. Bob chooses a secret integer b = 15, then sends Alice B = g^b mod p
   • B = 5¹⁵ mod 23 = 19
4. Alice computes s = B^a mod p
   • s = 19⁶ mod 23 = 2
5. Bob computes s = A^b mod p
   • s = 8¹⁵ mod 23 = 2
6. Alice and Bob now share a secret (the number 2).

/*
 this program calculates the Key
 for two persons
 using the Diffie Hellman Key exchange algorithm
*/
#include<stdio.h>
long long int power(int a,int b,int mod)
{
 long long int t;
 if(b==1)
  return a;
 t=power(a,b/2,mod);
 if(b%2==0)
  return (t*t)%mod;
 else
  return (((t*t)%mod)*a)%mod;
}
long long int calculateKey(int a,int x,int n)
{
 return power(a,x,n);
}
int main()
{
 int n,g,x,a,y,b;
 // both the persons will be agreed upon the common n and g
 printf("Enter the value of n and g : ");
 scanf("%d%d",&n,&g);

 // first person will choose the x
 printf("Enter the value of x for the first person : ");
 scanf("%d",&x);
 a=power(g,x,n);

 // second person will choose the y
 printf("Enter the value of y for the second person : ");
 scanf("%d",&y);
 b=power(g,y,n);

 printf("key for the first person is : %lld\n",power(b,x,n));
 printf("key for the second person is : %lld\n",power(a,y,n));
 return 0;
}

Reversing a Linked List using Recursion

#include<stdio.h>
#include<stdlib.h>

struct Node
{
	int data;
	struct Node*next;
};
struct Node*head;
struct Node*makeNode(int data)
{
	struct Node*node;
	node=(struct Node*)malloc(sizeof(struct Node));
	node->data=data;
	node->next=NULL;
	return node;
}
struct Node*insert(struct Node*start,struct Node*newNode)
{
	struct Node*ptr;
	if(start==NULL)
		return newNode;
	for(ptr=start;ptr->next;ptr=ptr->next);
	ptr->next=newNode;
	return start;
}
void printList(struct Node*start)
{
	struct Node*ptr;
	for(ptr=start;ptr;ptr=ptr->next)
		printf("%d ",ptr->data);
	printf("\n");
}
struct Node* reverseWithReturn(struct Node*node)
{
	struct Node*temp;
	if(node==NULL)
		return NULL;
	if(node->next==NULL)
		return node;
	temp=reverseWithReturn(node->next);
	node->next->next=node;
	node->next=NULL;
	return temp;
}
void reverseWithoutReturn(struct Node*node)
{
	/**
		for this function we need to maintain a global head
		this global head will be the head of new reversed list.

		this function will update the variable head
		now the head variable will store the start of newly formed list.
	*/
	if(node==NULL)
		return;
	if(node->next==NULL)
	{
		head=node;
		return ;
	}
	reverseWithoutReturn(node->next);
	node->next->next=node;
	node->next=NULL;
}
void reversePrint(struct Node*node)
{
	if(node==NULL)
		return;
	reversePrint(node->next);
	printf("%d ",node->data);
}
int main()
{
	struct Node*start;
	start=NULL;
	start=insert(start,makeNode(5));
	start=insert(start,makeNode(6));
	start=insert(start,makeNode(5));
	start=insert(start,makeNode(3));
	start=insert(start,makeNode(51));
	start=insert(start,makeNode(9));
	start=insert(start,makeNode(78));

	printList(start);
	start=reverseWithReturn(start);
	printList(start);

	return 0;
}

Hill Cipher - Program in C

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int **matrixMultiply(int**a,int r1,int c1,int **b,int r2,int c2)
{
 int **resultMatrix;
 int i,j,k,r,c;
 r=r1;c=c2;
 resultMatrix=(int**)malloc(sizeof(int*)*r);
 for(i=0;i<r;i++)
  resultMatrix[i]=(int*)malloc(sizeof(int)*c);
 for(i=0;i<r;i++)
 {
  for(j=0;j<c;j++)
  {
   resultMatrix[i][j]=0;
   for(k=0;k<c1;k++)
    resultMatrix[i][j]+=a[i][k]*b[k][j];
  }
 }
 return resultMatrix;
}
void printMatrix(int**matrix,int r,int c)
{
 int i,j;
 for(i=0;i<r;i++)
 {
  for(j=0;j<c;j++)
   printf("%d ",matrix[i][j]);
  printf("\n");
 }
}
int plainTextToCipherText(char plainText[],int**matrix)
{
 int len,**plainTextMatrix,**resultMatrix,i,j;
 // The matrix will be of dimensions strlen(plainText) by strlen(plainText)
 char *cipherText;
 len=strlen(plainText);
 cipherText=(char*)malloc(sizeof(char)*1000);

 // plainTextMatrix should be of dimension strlen(plainText) by 1
 // allcating memory to plainTextMatrix
 plainTextMatrix=(int**)malloc(sizeof(int*)*len);
 for(i=0;i<len;i++)
  plainTextMatrix[i]=(int*)malloc(sizeof(int)*1);

 // populating the plainTextMatrix
 for(i=0;i<len;i++)
  for(j=0;j<1;j++)
   plainTextMatrix[i][j]=plainText[i]-'a';

 resultMatrix=matrixMultiply(matrix,len,len,plainTextMatrix,len,1);
 
 // taking mod 26 of each element of the result matrix
 for(i=0;i<len;i++)
  for(j=0;j<1;j++)
   resultMatrix[i][j]%=26;

 // Printing the cipher text
 printf("The cipher text is as follows : ");
 for(i=0;i<len;i++)
  for(j=0;j<1;j++)
   printf("%c",resultMatrix[i][j]+'a');
 printf("\n");
 //printMatrix(resultMatrix,len,1);
}
int main()
{
 int len,i,j,**matrix;
 char plainText[1000];
 printf("Enter the word to be encrypted : ");
 scanf(" %s",plainText);
 len=strlen(plainText);

 // allocating memory to matrix
 matrix=(int**)malloc(sizeof(int*)*len);
 for(i=0;i<len;i++)
  matrix[i]=(int*)malloc(sizeof(int)*len);

 printf("Enter the matrix of %d by %d to be used in encryption process : \n",len,len);
 for(i=0;i<len;i++)
  for(j=0;j<len;j++)
   scanf("%d",&matrix[i][j]);

 plainTextToCipherText(plainText,matrix);
 return 0;
}

Caesar Cipher - Program in C

#include<stdio.h>
#include<stdlib.h>
char*plainTextToCipherText(char plainText[],int n)
{
 char *cipherText;
 int i;
 cipherText=(char*)malloc(sizeof(char)*1000);
 for(i=0;plainText[i];i++)
 {
  if(plainText[i]!=' ')
   cipherText[i]=((plainText[i]-'a'+n)%26)+'a';
  else
   cipherText[i]=plainText[i];
 }
 cipherText[i]='\0';
 return cipherText;
}
char*cipherTextToPlainText(char cipherText[],int n)
{
 char *plainText,c;
 int i;
 plainText=(char*)malloc(sizeof(char)*1000);
 for(i=0;cipherText[i];i++)
 {
  if(cipherText[i]!=' ')
  {
   c=(cipherText[i]-'a'-n)%26;
   if(c<0)
    c+=26;
   c+='a';
   plainText[i]=c;
  }
  else
  {
   plainText[i]=cipherText[i];
  }
 }
 plainText[i]='\0';
 return plainText;
}
int main()
{
 int n;
 char plainText1[1000],*cipherText1,cipherText2[1000],*plainText2;

 // Encoding Cipher Text
 printf("Enter the Plain Text (in lower case): ");
 scanf(" %[^\n]s",plainText1);
 printf("Enter the number of characters to be shifted : ");
 scanf("%d",&n);
 cipherText1=plainTextToCipherText(plainText1,n);
 printf("Cipher Text is : %s\n",cipherText1);


 // Decoding Plain Text
 printf("\nEnter the Cipher Text (in lower case) : ");
 scanf(" %[^\n]s",cipherText2);
 printf("Enter the number of charaters to be shifted : ");
 scanf("%d",&n);
 plainText2=cipherTextToPlainText(cipherText2,n);
 printf("The Plain Text is : %s\n",plainText2);
 return 0;
}

Generic Representation of Graph - Generic List of Vertices and Edges

LinkedList_Generic.h

struct LinkedList_Generic
{
 struct ListNode_Generic*start;
 int elementSize;
 /*
  elementSize, will store the size of each element. 
  The element size is important, because generics in C are limited to void pointers, 
  in order to let the compiler know the amount of memory needed by malloc/memcpy. 
  This information should always be supplied dynamically. The caller should use sizeof(int) rather than 4.
 */
};
struct ListNode_Generic
{
 void *data;
 struct ListNode_Generic*next;
};
struct LinkedList_Generic *makeAndInitialiseLinkedList();
struct ListNode_Generic *makeAndInitialiseListNode(struct LinkedList_Generic *list,void*element);
void addElement(struct LinkedList_Generic*list,struct ListNode_Generic*element);
void removeElement(struct LinkedList_Generic*list,struct ListNode_Generic*node);
struct ListNode_Generic*getNodeReferenceWithGivenData(struct LinkedList_Generic*list,void*data);

LinkedList_Generic.c

#include<stdlib.h>
#include<string.h>
#include"LinkedList_Generic.h"

struct LinkedList_Generic *makeAndInitialiseLinkedList(int elementSize)
{
 struct LinkedList_Generic *list;
 list=(struct LinkedList_Generic*)malloc(sizeof(struct LinkedList_Generic));
 list->start=NULL;
 list->elementSize=elementSize;
 return list;
}
struct ListNode_Generic *makeAndInitialiseListNode(struct LinkedList_Generic *list,void*element)
{
 struct ListNode_Generic*listNode;
 listNode=(struct ListNode_Generic*)malloc(sizeof(struct ListNode_Generic));
 listNode->data=element;
 //listNode->data=malloc(sizeof(list->elementSize));
 //memcpy(listNode->data,element,list->elementSize);
 listNode->next=NULL;
 return listNode;
}
void addElement(struct LinkedList_Generic*list,struct ListNode_Generic*element)
{
 struct ListNode_Generic*ptr,*prev;
 if((list->start)==NULL)
  (list->start)=element;
 else
 {
  for(ptr=(list->start);ptr;prev=ptr,ptr=ptr->next);
  (prev->next)=element;
 }
}
void removeElement(struct LinkedList_Generic*list,struct ListNode_Generic*node)
{
 struct ListNode_Generic*ptr,*prev;
 for(ptr=(list->start),prev=NULL;ptr && (ptr)!=node;prev=ptr,ptr=ptr->next);
 if(ptr)
 {
  if(prev!=NULL)
  {
   prev->next=ptr->next;
   if(ptr)
   {
    free(ptr);
   }
  }
  else if(prev==NULL && ptr!=NULL) // means the element that we need to delete is the start of the list.
  {
   prev=list->start;
   (list->start)=((list->start)->next);
   if(prev)
   {
    free(prev);
   }
  }
 }
}
struct ListNode_Generic*getNodeReferenceWithGivenData(struct LinkedList_Generic*list,void*data)
{
 struct ListNode_Generic*node;
 for(node=list->start;node;node=node->next)
 {
  if((node->data)==data)
   return node;
 }
}

Graph_Generic.h

struct Graph_Generic
{
 struct LinkedList_Generic *vertexList,*edgeList;
 int numberOfVertices, numberOfEdges;
};
struct Vertex
{
 int id;
 int inDegree,outDegree;
};
struct Edge
{
 int id,sourceVertex,destinationVertex,isDirected,weight;
};
struct Graph_Generic*makeAndInitialiseGraph();
void addVertex(struct Graph_Generic*graph,struct Vertex*vertex);
void removeVertex(struct Graph_Generic*graph,int vertexNumber);
void addEdge(struct Graph_Generic*graph,struct Edge*edge);
void removeEdge(struct Graph_Generic *graph,int ,int ,int);
struct Edge *makeEdge(int sourceVertex,int destinationVertex,int weight,int isDirected);
struct Vertex *makeVertex();
void printGraph_Generic(struct Graph_Generic*grpah);

Graph_Generic.c

#include"Graph_Generic.h"
#include"LinkedList_Generic.h"
#include<stdlib.h>
#include<stdio.h>
struct Graph_Generic*makeAndInitialiseGraph()
{
 struct Graph_Generic*graph;
 graph=(struct Graph_Generic*)malloc(sizeof(struct Graph_Generic));
 graph->numberOfVertices=0;
 graph->numberOfEdges=0;
 graph->vertexList=makeAndInitialiseLinkedList(sizeof(struct Vertex));
 graph->edgeList=makeAndInitialiseLinkedList(sizeof(struct Edge));
 return graph;
}
struct Edge *makeEdge(int sourceVertex,int destinationVertex,int weight,int isDirected)
{
 static int edgeNumber=0;
 struct Edge*edge;
 edge=(struct Edge*)malloc(sizeof(struct Edge));
 edge->sourceVertex=sourceVertex;
 edge->destinationVertex=destinationVertex; 
 edge->weight=weight;
 edge->isDirected=isDirected;
 edge->id=edgeNumber++;
 return edge;
}
struct Vertex *makeVertex()
{
 static int vertexNumber=0;
 struct Vertex*vertex;
 vertex=(struct Vertex*)malloc(sizeof(struct Vertex));
 (vertex->id)=vertexNumber++;
 return vertex;
}

void addVertex(struct Graph_Generic*graph,struct Vertex*vertex)
{
 (graph->numberOfVertices)++;
 addElement(graph->vertexList,makeAndInitialiseListNode(graph->vertexList,vertex));
}
void removeVertex(struct Graph_Generic*graph,int vertexNumber)
{
 struct Edge*e;
 struct ListNode_Generic*ptr,*ptr1;
 (graph->numberOfVertices)--;
 for(ptr=graph->vertexList->start;ptr;ptr=ptr->next)
 {
  if(((struct Vertex*)(ptr->data))->id==vertexNumber)
   break;
 }
 if(ptr)
 {
  /*
   when you will be deleting an vertex then all the edges from and to that vertex should be deleted.
  */
  for(ptr1=graph->edgeList->start;ptr1;ptr1=ptr1->next)
  {
   e=(struct Edge*)(ptr1->data);
   if(e->sourceVertex==vertexNumber || e->destinationVertex==vertexNumber)
    removeEdge(graph,e->sourceVertex,e->destinationVertex,e->weight);
  }
  removeElement(graph->vertexList,ptr);
 }
}
void addEdge(struct Graph_Generic*graph,struct Edge*edge)
{
 (graph->numberOfEdges)++;
 addElement(graph->edgeList,makeAndInitialiseListNode(graph->edgeList,edge));
}
void removeEdge(struct Graph_Generic *graph,int sourceVertex,int destinationVertex,int weight)
{
 struct ListNode_Generic*ptr;
 (graph->numberOfEdges)--;
 for(ptr=(graph->edgeList->start);ptr;ptr=ptr->next)
 {
  if(
   ((struct Edge*)(ptr->data))->sourceVertex==sourceVertex &&
   ((struct Edge*)(ptr->data))->destinationVertex==destinationVertex &&
   ((struct Edge*)(ptr->data))->weight==weight
  ) break;
 }
 if(ptr)
  removeElement(graph->edgeList,ptr);
}
void printGraph_Generic(struct Graph_Generic*graph)
{
 int i;
 struct ListNode_Generic*ptr;
 printf("\nPrinting the vertex List : \n");
 printf("\nTotal Number Of Vertices in the Graph : %d\n",graph->numberOfVertices);
 for(ptr=(struct ListNode_Generic*)((graph->vertexList)->start);ptr;ptr=ptr->next)
  printf("%d ",((struct Vertex*)(ptr->data))->id);
 printf("\nTotal Number Of Edges in the Graph : %d\n",graph->numberOfEdges);
 for(ptr=(struct ListNode_Generic*)((graph->edgeList)->start);ptr;ptr=ptr->next)
  printf("Edge No. : %d, from %d to %d with weight=%d and isDirected?=%d\n",((struct Edge*)(ptr->data))->id,((struct Edge*)(ptr->data))->sourceVertex,((struct Edge*)(ptr->data))->destinationVertex,((struct Edge*)(ptr->data))->weight,((struct Edge*)(ptr->data))->isDirected);
}

main.c

#include<stdio.h>
#include"Graph_Generic.h"
int main()
{
 struct Graph_Generic*graph;
 int a,b,weight,isDirected,i,numberOfVertices,numberOfEdges,sourceVertex,destinationVertex,vertexNumber;

 printf("Enter the number of Vertices in the Graph : ");
 scanf("%d",&(numberOfVertices));
 printf("Enter the number of Edges in the Graph : ");
 scanf("%d",&(numberOfEdges));

 graph=makeAndInitialiseGraph();

 for(i=0;i<numberOfVertices;i++)
  addVertex(graph,makeVertex());

 printf("NOTE 1 : The ordering of the Vertices and Edges is zero indexed.\n");
 printf("NOTE 2 : For each edge enter the following in Sequence : \n");
 printf("\t1. Source Vertex Number.\n");
 printf("\t2. Destination Vertex Number.\n");
 printf("\t3. Weight associated with Edge.\n");
 printf("\t4. 1 if the Edge is Directed, and 0 otherwise.\n");
 
 for(i=0;i<numberOfEdges;i++)
 {
  printf("Enter the edge Number %d : ",i+1);
  scanf("%d%d%d%d",&a,&b,&weight,&isDirected);
  addEdge(graph,makeEdge(a,b,weight,isDirected));
 }
 printGraph_Generic(graph);
 
 printf("\nDeleting an Edge : \n");
 printf("Enter the sourceVertex, destinationVertex and weight of the graph : ");
 scanf("%d%d%d",&sourceVertex,&destinationVertex,&weight);
 removeEdge(graph,sourceVertex,destinationVertex,weight);
 
 printf("Deleting a Vertex : \n");
 printf("Enter the Vertex number to be deleted : ");
 scanf("%d",&vertexNumber);
 removeVertex(graph,vertexNumber);
 
 printGraph_Generic(graph);
 
 printf("Program Execution Successful...\n");
 return 0;
}

Makefile

all: LinkedList_Generic.o Graph_Generic.o main.o
 gcc LinkedList_Generic.o Graph_Generic.o main.o -o hello
LinkedList_Generic.o: LinkedList_Generic.c
 gcc -c LinkedList_Generic.c
Graph_Generic.o: Graph_Generic.c
 gcc -c Graph_Generic.c
main.o: main.c
 gcc -c main.c
clean:
 rm -rf *.o *~ hello

SampleInputData.txt

6
9
1 0 1 1
1 3 1 1
1 2 1 1 
0 5 1 1
0 4 1 1
2 3 1 1
2 4 1 1
2 5 1 1
4 3 1 1
2 5 1
0

Adjacency Matrix Representation of Graph

one_D_bit_array.h

int get_one_D_bit_array(int ,int *);
void reset_one_D_bit_array(int ,int *);
void set_one_D_bit_array(int ,int *);

one_D_bit_array.c

#include"one_D_bit_array.h"
int get_one_D_bit_array(int i,int* arr)
{
 if((arr[i/32]&((unsigned int)1<<(31-i%32)))!=0)
  return 1;
 return 0;
}
void set_one_D_bit_array(int i,int *arr)
{
 arr[i/32]|=((unsigned int)1<<(31-i%32));  // to set its 31-(n%32) th bit.
}
void reset_one_D_bit_array(int i,int *arr)
{
 arr[i/32]&=(~((unsigned int)1<<(31-i%32))); // to reset its 31-(n%32) th bit.
}

two_D_bit_array.h

int get_two_D_bit_array(int ,int ,int *,int);
void set_two_D_bit_array(int ,int ,int *,int);
void reset_two_D_bit_array(int ,int ,int *,int);

two_D_bit_array.c

#include"two_D_bit_array.h"

/*  
  this function will return bit value in 
  ith row and 
  jth column
  from the array 'arr'
  which provides an abstraction of 2-D bit array of size n * n.
*/ 
int get_two_D_bit_array(int i,int j,int* arr,int n)
{
 int bitNumber=i*n+j;
 if((arr[bitNumber/32]&((unsigned int)1<<(31-bitNumber%32)))!=0)
  return 1;
 return 0;
}

/*  
  this function will set the bit value in 
  ith row and 
  jth column
  in the array 'arr'
  which provides an abstraction of 2-D bit array of size n * n
  to 1.
*/ 
void set_two_D_bit_array(int i,int j,int *arr,int n)
{ 
 int bitNumber=i*n+j;
 arr[bitNumber/32]|=((unsigned int)1<<(31-bitNumber%32));  // to set its 31-(bitNumber%32) th bit.
}

/*  
  this function will set the bit value in 
  ith row and 
  jth column
  in the array 'arr'
  which provides an abstraction of 2-D bit array of size n * n
  to 0.
*/ 
void reset_two_D_bit_array(int i,int j,int *arr,int n)
{
 int bitNumber=i*n+j;
 arr[bitNumber/32]&=(~((unsigned int)1<<(31-bitNumber%32))); // to reset its 31-(bitNumber%32) th bit.
}

Graph_AdjacencyMatrix.h

struct Graph
{
 int numberOfVertices,numberOfEdges;
 unsigned int*adjacencyMatrix;
};
struct Graph*makeNewGraph();
void initializeAdjacencyMatrix(struct Graph*);
void createEdge(struct Graph*,int,int);
void removeEdge(struct Graph*,int,int);
void showAdjacencyMatrix(struct Graph*);
int findNumberOfComponents(struct Graph*);

Graph_AdjacencyMatrix.c

#include<stdio.h>
#include<stdlib.h>
#include"Graph_AdjacencyMatrix.h"
#include"two_D_bit_array.h"
#include"one_D_bit_array.h"

struct Graph*makeNewGraph()
{
 struct Graph*g;
 g=(struct Graph*)malloc(sizeof(struct Graph));
 return g;
}
void initializeAdjacencyMatrix(struct Graph*g)
{
 /*
  The adjacencyMatrix corresponding to vertex u and v will contain 1 if there is an edge from u to v
  otherwise it will contain 0

  Description of data structure used for making adjacencyMatrix:
   * We will need n*n bits to represent the existence of an edge between two vertices
   * These n*n bits should be assumed to be arranged in the linear fashion
   * For implementing this linear fashion we will use an array of integers.
   * For a standard 32 bit compiler (like gcc 4.8.2) size of an integer is 32 bits (4 bytes).
   * By this linear arrangement of AdjacencyMatrix we will optimally exploit every single bit.
 */
 int sizeOfIntegerColumns,i,j;
 sizeOfIntegerColumns=((g->numberOfVertices)*(g->numberOfVertices))/32+1;
 (g->adjacencyMatrix)=(unsigned int*)malloc(sizeof(unsigned int)*sizeOfIntegerColumns);
 for(i=0;i<sizeOfIntegerColumns;i++)
  (g->adjacencyMatrix)[i]=0;
}
void createEdge(struct Graph*g,int a,int b)
{
 set_two_D_bit_array(a,b,g->adjacencyMatrix,g->numberOfVertices);
}
void removeEdge(struct Graph*g,int a,int b)
{
 reset_two_D_bit_array(a,b,g->adjacencyMatrix,g->numberOfVertices);
}
void showAdjacencyMatrix(struct Graph*g)
{
 int i,j,bitNumber;
 printf("The adjacency Matrix of the Graph is as follows : \n");
 for(i=0;i<(g->numberOfVertices);i++)
 {
  for(j=0;j<(g->numberOfVertices);j++)
   printf("%d",get_two_D_bit_array(i,j,g->adjacencyMatrix,g->numberOfVertices));
  printf("\n");
 }
}

int findNumberOfComponents(struct Graph*g)
{
 /*
  first of all we need to create a copy of the AdjacencyMatrix.
 */
 unsigned int *adjacencyMatrix_copy,*flag,sizeOfIntegerColumns,i,j,k,components;
 sizeOfIntegerColumns=((g->numberOfVertices)*(g->numberOfVertices))/32+1;
 adjacencyMatrix_copy=(unsigned int*)malloc(sizeof(unsigned int)*sizeOfIntegerColumns);
 for(i=0;i<sizeOfIntegerColumns;i++)
  adjacencyMatrix_copy[i]=(g->adjacencyMatrix)[i];
 /* copy of adjacencyMatrix created */

 /*  now we need to keep the track of vertices being merged
  for this we need to introduce a one-D bit array that will keep track of this information.
  let this one-D bit array be flag.
 */
 flag=(unsigned int *)malloc(sizeof(unsigned int)*(g->numberOfVertices)/32+1);
 for(i=0;i<(g->numberOfVertices)/32+1;i++)
  flag[i]=0;
 /*
  if the nth bit of flag array is 0 this means that the vertex with vertexNumber 'n' is still
  alive and is not merged with any other vertex.

  if the nth bit of flag array is 1 this means that the vertex with vertexNumber 'n' is dead
  and is merged with some other vertex and has no existence now.
 */
 /* now we are ready for merging vertices in our dummy (copied) adjacencyMatrix.  */
 for(i=0;i<(g->numberOfVertices);i++)
 {
  if(get_one_D_bit_array(i,flag)==0) // means ith vertex is alive
  {
   for(j=0;j<(g->numberOfVertices);j++)
   {
    if(j!=i && get_one_D_bit_array(j,flag)==0) // means the jth vertex is alive
    {
     if(get_two_D_bit_array(i,j,adjacencyMatrix_copy,g->numberOfVertices)==1)
     {
      /*
       now we need to merge the ith node with the jth node
       for this we need to merge
        ith row with jth row, and
        ith col with jth col
      */
      for(k=0;k<(g->numberOfVertices);k++) // merging the ith and jth rows
      {
       if(get_two_D_bit_array(i,k,adjacencyMatrix_copy,g->numberOfVertices) | get_two_D_bit_array(j,k,adjacencyMatrix_copy,g->numberOfVertices))
        set_two_D_bit_array(i,k,adjacencyMatrix_copy,g->numberOfVertices);
      }
      for(k=0;k<(g->numberOfVertices);k++) // merging the ith and jth cols
      {
       if(get_two_D_bit_array(k,i,adjacencyMatrix_copy,g->numberOfVertices) | get_two_D_bit_array(k,j,adjacencyMatrix_copy,g->numberOfVertices))
        set_two_D_bit_array(k,i,adjacencyMatrix_copy,g->numberOfVertices);
      }
      /* now the jth vertex is merged with ith vertex so the ith vertex should have no existence */
      /* so we need to set the jth bit of flag array to 1 */
      set_one_D_bit_array(j,flag); // declaring that the jth vertex is now dead.
     }
    }
   }
  }
 }
 /* 
  now the total number of components in the graph will be the number of vertices that still have zero 
  correponding to their vertex number in flag array.
 */
 components=0;
 for(i=0;i<(g->numberOfVertices);i++)
  if(get_one_D_bit_array(i,flag)==0)
   components++;
 return components;
}

main.c

#include<stdio.h>
#include"Graph_AdjacencyMatrix.h"

int main()
{
 int i,n,a,b;
 struct Graph*g;
 g=makeNewGraph();
 printf("Enter the number of Vertices in the Graph : ");
 scanf("%d",&(g->numberOfVertices));
 printf("Enter the number of Edges in the Graph : ");
 scanf("%d",&(g->numberOfEdges));
 initializeAdjacencyMatrix(g);
 printf("NOTE : The ordering of the vertices is zero indexed.\n");
 for(i=0;i<(g->numberOfEdges);i++)
 {
  printf("Enter the edge Number %d : ",i+1);
  scanf("%d%d",&a,&b);
  createEdge(g,a,b);
 }
 showAdjacencyMatrix(g);
 printf("Number of components in the Graph = %d\n",findNumberOfComponents(g));
 printf("\nProgram execution successful...\n");
 return 0;
}

Makefile

all: hello
hello: one_D_bit_array.o two_D_bit_array.o Graph_AdjacencyMatrix.o main.o
 gcc one_D_bit_array.o two_D_bit_array.o Graph_AdjacencyMatrix.o main.o -o hello
one_D_bit_array.o: one_D_bit_array.c
 gcc -c one_D_bit_array.c
two_D_bit_array.o: two_D_bit_array.c
 gcc -c two_D_bit_array.c
main.o: main.c
 gcc -c main.c
graph.o: Graph_AdjacencyMatrix.c
 gcc -c Graph_AdjacencyMatrix.c
clean:
 rm -rf *~ *.o hello

SampleTestData.txt

4
8
0 2
2 0
1 3
3 1
0 3
3 0
3 2
2 3

Adjacency List Representation of Graph

LinkedList_Generic.h

struct LinkedList_Generic
{
 struct ListNode_Generic*start;
 int elementSize;
 /*
  elementSize, will store the size of each element. 
  The element size is important, because generics in C are limited to void pointers, 
  in order to let the compiler know the amount of memory needed by malloc/memcpy. 
  This information should always be supplied dynamically. The caller should use sizeof(int) rather than 4.
 */
};
struct ListNode_Generic
{
 void *data;
 struct ListNode_Generic*next;
};
struct LinkedList_Generic *makeAndInitialiseLinkedList();
struct ListNode_Generic *makeAndInitialiseListNode(struct LinkedList_Generic *list,void*element);
void addElement(struct LinkedList_Generic*list,struct ListNode_Generic*element);
void removeElement(struct LinkedList_Generic*list,struct ListNode_Generic*node);
struct ListNode_Generic*getNodeReferenceWithGivenData(struct LinkedList_Generic*list,void*data);

LinkedList_Generic.c

#include<stdlib.h>
#include<string.h>
#include"LinkedList_Generic.h"

struct LinkedList_Generic *makeAndInitialiseLinkedList(int elementSize)
{
 struct LinkedList_Generic *list;
 list=(struct LinkedList_Generic*)malloc(sizeof(struct LinkedList_Generic));
 list->start=NULL;
 list->elementSize=elementSize;
 return list;
}
struct ListNode_Generic *makeAndInitialiseListNode(struct LinkedList_Generic *list,void*element)
{
 struct ListNode_Generic*listNode;
 listNode=(struct ListNode_Generic*)malloc(sizeof(struct ListNode_Generic));
 listNode->data=element;
 //listNode->data=malloc(sizeof(list->elementSize));
 //memcpy(listNode->data,element,list->elementSize);
 listNode->next=NULL;
 return listNode;
}
void addElement(struct LinkedList_Generic*list,struct ListNode_Generic*element)
{
 struct ListNode_Generic*ptr,*prev;
 if((list->start)==NULL)
  (list->start)=element;
 else
 {
  for(ptr=(list->start);ptr;prev=ptr,ptr=ptr->next);
  (prev->next)=element;
 }
}
void removeElement(struct LinkedList_Generic*list,struct ListNode_Generic*node)
{
 struct ListNode_Generic*ptr,*prev;
 for(ptr=(list->start),prev=NULL;ptr && (ptr)!=node;prev=ptr,ptr=ptr->next);
 if(ptr)
 {
  if(prev!=NULL)
  {
   prev->next=ptr->next;
   if(ptr)
   {
    free(ptr);
   }
  }
  else if(prev==NULL && ptr!=NULL) // means the element that we need to delete is the start of the list.
  {
   prev=list->start;
   (list->start)=((list->start)->next);
   if(prev)
   {
    free(prev);
   }
  }
 }
}
struct ListNode_Generic*getNodeReferenceWithGivenData(struct LinkedList_Generic*list,void*data)
{
 struct ListNode_Generic*node;
 for(node=list->start;node;node=node->next)
 {
  if((node->data)==data)
   return node;
 }
}

Graph_AdjacencyList.h

#include"LinkedList_Generic.h"
struct Graph_AdjacencyList
{
 struct LinkedList_Generic *vertexList;
 int numberOfVertices;
};
struct Vertex_AdjacencyList
{
 int id;
 struct LinkedList_Generic *adjacencyList;
};
struct Graph_AdjacencyList*makeAndInitialiseGraph();
void addVertex(struct Graph_AdjacencyList*graph,struct Vertex_AdjacencyList*vertex);
int getVertexId(struct ListNode_Generic*node);
void removeVertex(struct Graph_AdjacencyList*graph,int vertexNumber);
void addEdge(struct Graph_AdjacencyList*graph,int sourceVertexNumber,int destinationVertexNumber);
void removeEdge(struct Graph_AdjacencyList *graph,int sourceVertexNumber,int destinationVertexNumber);
struct Vertex_AdjacencyList *makeVertex();
void printGraph_AdjacencyList(struct Graph_AdjacencyList*graph);

Graph_AdjacencyList.c

/*
 This representation of graph is the Adjacency List representation.
 Corresponding to each vertex of the graph we maintain a list of vertices that are connected to that vertex.
 for maintaining the vertex list (adjacency List) corresponding to each vertex, we maintain a Generic List.
 this generic list is defined in LinkedList_Generic.c
 
 this adjacencyList corresponding to each vertex will just store the references of vertex (reference of c, don't get confused with the reference variables of c++)
 
 this storing of reference will have the following advantage :
  Suppose you need to modify any of the data for a specific vertex, then you just need to modify the data correnponding to that vertex in the vertex list.
  you dont need to modify each and every node where this vertex may apper in the adjacencyList of any vertex.
*/

#include"Graph_AdjacencyList.h"
#include<stdlib.h>
#include<stdio.h>
struct Graph_AdjacencyList*makeAndInitialiseGraph()
{
 struct Graph_AdjacencyList*graph;
 graph=(struct Graph_AdjacencyList*)malloc(sizeof(struct Graph_AdjacencyList));
 graph->numberOfVertices=0;
 graph->vertexList=makeAndInitialiseLinkedList(sizeof(struct Vertex_AdjacencyList));
 return graph;
}
struct Vertex_AdjacencyList *makeVertex()
{
 static int vertexNumber=0;
 struct Vertex_AdjacencyList*vertex;
 vertex=(struct Vertex_AdjacencyList*)malloc(sizeof(struct Vertex_AdjacencyList));
 (vertex->id)=vertexNumber++;
 vertex->adjacencyList=makeAndInitialiseLinkedList(sizeof(struct Vertex_AdjacencyList*));
 return vertex;
}
struct Vertex_AdjacencyList*getVertexReference(struct Graph_AdjacencyList*graph,int n)
{
 struct Vertex_AdjacencyList*vertex;
 struct ListNode_Generic*node;
 for(node=graph->vertexList->start;node;node=node->next)
 {
  vertex=(struct Vertex_AdjacencyList*)(node->data);
  if(vertex->id==n)
   return vertex;
 }
}
void addVertex(struct Graph_AdjacencyList*graph,struct Vertex_AdjacencyList*vertex)
{
 (graph->numberOfVertices)++;
 addElement(graph->vertexList,makeAndInitialiseListNode(graph->vertexList,vertex));
}

void removeVertex(struct Graph_AdjacencyList*graph,int vertexNumber)
{
 int i;
 struct ListNode_Generic*node;
 struct Vertex_AdjacencyList*vertex;
 for(node=graph->vertexList->start;node;node=node->next)
 {
  vertex=(struct Vertex_AdjacencyList*)(node->data);
  removeEdge(graph,vertex->id,vertexNumber);
 }
 removeElement(graph->vertexList,getNodeReferenceWithGivenData(graph->vertexList,getVertexReference(graph,vertexNumber)));
}

void addEdge(struct Graph_AdjacencyList*graph,int sourceVertexNumber,int destinationVertexNumber)
{
 addElement
 (
  getVertexReference(graph,sourceVertexNumber)->adjacencyList,
  makeAndInitialiseListNode
  (
   getVertexReference(graph,sourceVertexNumber)->adjacencyList,
   getVertexReference(graph,destinationVertexNumber)
  )
 );
}
void removeEdge(struct Graph_AdjacencyList *graph,int sourceVertexNumber,int destinationVertexNumber)
{
 removeElement
 (
  getVertexReference(graph,sourceVertexNumber)->adjacencyList,
  getNodeReferenceWithGivenData
  (
   getVertexReference(graph,sourceVertexNumber)->adjacencyList,
   getVertexReference(graph,destinationVertexNumber)
  )
 );
}
void printGraph_AdjacencyList(struct Graph_AdjacencyList*graph)
{
 struct Vertex_AdjacencyList*vertexPtr,*jointVertex;
 struct ListNode_Generic*pointer,*ptr;
 int i;
 printf("\nTotal Number Of Vertices in the Graph : %d\n",graph->numberOfVertices);
 printf("\nPrinting the Adjacency List of each vertex. \n");
 for(ptr=(struct ListNode_Generic*)((graph->vertexList)->start);ptr;ptr=ptr->next)
 {
  vertexPtr=(struct Vertex_AdjacencyList*)(ptr->data);
  printf("Vertex No. : %d: ",vertexPtr->id); // Printing the id of current vertex number.
  for(pointer=(struct ListNode_Generic*)((vertexPtr->adjacencyList)->start);pointer;pointer=pointer->next)
  {
   jointVertex=(struct Vertex_AdjacencyList*)(pointer->data);
   printf("%d ",jointVertex->id);
  }
  printf("\n\n");
 }
}

main.c

#include<stdio.h>
#include"Graph_AdjacencyList.h"
int main()
{
 struct Graph_AdjacencyList*graph;
 int a,b,weight,isDirected,i,numberOfVertices,numberOfEdges,sourceVertexNumber,destinationVertexNumber,vertexNumber;

 printf("Enter the number of Vertices in the Graph : ");
 scanf("%d",&(numberOfVertices));
 printf("Enter the number of Edges in the Graph : ");
 scanf("%d",&(numberOfEdges));

 graph=makeAndInitialiseGraph();

 for(i=0;i<numberOfVertices;i++)
  addVertex(graph,makeVertex());

 printf("NOTE 1 : The ordering of the Vertices and Edges is zero indexed.\n");
 printf("NOTE 2 : For each edge enter the following in Sequence : \n");
 printf("\t1. Source Vertex Number.\n");
 printf("\t2. Destination Vertex Number.\n");
 
 for(i=0;i<numberOfEdges;i++)
 {
  printf("Enter the edge Number %d : ",i+1);
  scanf("%d%d",&a,&b);
  addEdge(graph,a,b);
 }
 printGraph_AdjacencyList(graph);
 
 /* Deleting an Edge */
 printf("To Remove an Edge Enter the source and destination vertex number : ");
 scanf("%d%d",&sourceVertexNumber,&destinationVertexNumber);
 removeEdge(graph,sourceVertexNumber,destinationVertexNumber);
 printGraph_AdjacencyList(graph);
 
 /* Deleting a Vertex */
 printf("To delete a vertex enter the vertex number :");
 scanf("%d",&vertexNumber);
 removeVertex(graph,vertexNumber);
 printGraph_AdjacencyList(graph);
 printf("Program Execution Successful...\n");
 return 0;
}

Makefile

all: LinkedList_Generic.o Graph_AdjacencyList.o main.o
 gcc LinkedList_Generic.o Graph_AdjacencyList.o main.o -o hello
LinkedList_Generic.o: LinkedList_Generic.c
 gcc -c LinkedList_Generic.c
Graph_AdjacencyList.o: Graph_AdjacencyList.c
 gcc -c Graph_AdjacencyList.c
main.o: main.c
 gcc -c main.c
clean :
 rm -rf *~ *.o hello

SampleTest.txt

4
8
0 2
2 0
3 0
0 3
2 3
3 2
3 1
1 3

2 0

3

FIND THE NUMBER OF COMPONENTS IN A GRAPH : ADJACENCY MATRIX REPRESENTATION - MERGING NODES

Write a program to check whether given graph is connected or not. Compute number of components for disconnected graph.

In graph theory, a connected component (or just component) of an undirected graph is a sub-graph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices in the super-graph.

For example the following graph has 3 components.

Clearly if a graph has a total of only one component, then the graph is called Connected, and on the other hand if the graph has more than one component then the graph is called Disconnected graph.

The following program finds the number of components in a graph. For representing a graph, I have used here the Adjacency Matrix representation of Graph.

Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. If the adjacency matrix has an entry of 1 corresponding to the ith row and jth column, this means that there is an edge from the ith vertex to the jth vertex.

No, doubt we will need V x V bits in total to store the adjacency matrix of the graph, where V is the number of vertices. Note that many novice programmers will create an integer array of size V x V which will definitely lead to wastage of memory because every entry in the adjacency matrix is either 0 or 1, 0 representing no edge and 1 representing an edge. And because of this nature of the adjacency matrix we don't need to have an integer array when we can do the same task in a 2D bit array. This is what I have exactly done in the following program.

Now an obvious question will be that how to maintain a 2D bit array in a programming language like C. For this I have a 1D integer array, in which i will utilize each and every single bit to represent an edge between two vertices.

I will explain this using an example.

Suppose you have a graph of 5 vertices, the size of your adjacency list will be 25 bits. And we know that in a 32 bit C compiler (like gcc 4.8.2) these all 25 bits could be accommodated in a single integer, saving an enormous amount of memory.

But suppose you have 10 vertices, so then the size of your adjacency matrix will be 100 bits, which could be easily (and surely) accommodated in 4 integers, so the size of your adjacency matrix will be just 4 integers.

I think I have made myself clear, all the readers have got the concept and from now they will definitely appreciate concept of bit representation of the adjacency matrix.

The reader should note here that this representation is applicable only when the graph is un-weighted, that is there are no associated weights with the edges, otherwise this representation will not work.

Now I would like to explain the algorithm for finding the number of components in a graph given the adjacency matrix of the graph.

The basic idea of this algorithm is to merge adjacent vertices of the graph. We start with a vertex in the graph and merge all the adjacent vertices. Then we take the newly formed vertex after merging and again merge all the vertices that are adjacent to it. And we continue this step until no more merging is possible. After the exhaustive step when no more merging is possible, the number of remaining vertices will denote the number of components in the original graph.

Here I would like to add that, in adjacency matrix merging of ith vertex with the jth vertex can be accomplished by bit-wise OR operation, and I have followed the same in the source code presented below.

Here is the source code of all the things that I explained to you in above paragraphs:

one_D_bit_array.h

int get_one_D_bit_array(int ,int *);
void reset_one_D_bit_array(int ,int *);
void set_one_D_bit_array(int ,int *);

one_D_bit_array.c

#include"one_D_bit_array.h"
int get_one_D_bit_array(int i,int* arr)
{
 if((arr[i/32]&((unsigned int)1<<(31-i%32)))!=0)
  return 1;
 return 0;
}
void set_one_D_bit_array(int i,int *arr)
{
 arr[i/32]|=((unsigned int)1<<(31-i%32));  // to set its 31-(n%32) th bit.
}
void reset_one_D_bit_array(int i,int *arr)
{
 arr[i/32]&=(~((unsigned int)1<<(31-i%32))); // to reset its 31-(n%32) th bit.
}

two_D_bit_array.h

int get_two_D_bit_array(int ,int ,int *,int);
void set_two_D_bit_array(int ,int ,int *,int);
void reset_two_D_bit_array(int ,int ,int *,int);

two_D_bit_array.c

#include"two_D_bit_array.h"

/*  
  this function will return bit value in 
  ith row and 
  jth column
  from the array 'arr'
  which provides an abstraction of 2-D bit array of size n * n.
*/ 
int get_two_D_bit_array(int i,int j,int* arr,int n)
{
 int bitNumber=i*n+j;
 if((arr[bitNumber/32]&((unsigned int)1<<(31-bitNumber%32)))!=0)
  return 1;
 return 0;
}

/*  
  this function will set the bit value in 
  ith row and 
  jth column
  in the array 'arr'
  which provides an abstraction of 2-D bit array of size n * n
  to 1.
*/ 
void set_two_D_bit_array(int i,int j,int *arr,int n)
{ 
 int bitNumber=i*n+j;
 arr[bitNumber/32]|=((unsigned int)1<<(31-bitNumber%32));  // to set its 31-(bitNumber%32) th bit.
}

/*  
  this function will set the bit value in 
  ith row and 
  jth column
  in the array 'arr'
  which provides an abstraction of 2-D bit array of size n * n
  to 0.
*/ 
void reset_two_D_bit_array(int i,int j,int *arr,int n)
{
 int bitNumber=i*n+j;
 arr[bitNumber/32]&=(~((unsigned int)1<<(31-bitNumber%32))); // to reset its 31-(bitNumber%32) th bit.
}

graph.h

struct Graph
{
 int numberOfVertices,numberOfEdges;
 unsigned int*adjacencyMatrix;
};
struct Graph*makeNewGraph();
void initializeAdjacencyMatrix(struct Graph*);
void createEdge(struct Graph*,int,int);
void removeEdge(struct Graph*,int,int);
void showAdjacencyMatrix(struct Graph*);
int findNumberOfComponents(struct Graph*);

graph.c

#include<stdio.h>
#include<stdlib.h>
#include"Graph_AdjacencyMatrix.h"
#include"two_D_bit_array.h"
#include"one_D_bit_array.h"

struct Graph*makeNewGraph()
{
	struct Graph*g;
	g=(struct Graph*)malloc(sizeof(struct Graph));
	return g;
}
void initializeAdjacencyMatrix(struct Graph*g)
{
	/*
		The adjacencyMatrix corresponding to vertex u and v will contain 1 if there is an edge from u to v
		otherwise it will contain 0

		Description of data structure used for making adjacencyMatrix:
			* We will need n*n bits to represent the existence of an edge between two vertices
			* These n*n bits should be assumed to be arranged in the linear fashion
			* For implementing this linear fashion we will use an array of integers.
			* For a standard 32 bit compiler (like gcc 4.8.2) size of an integer is 32 bits (4 bytes).
			* By this linear arrangement of AdjacencyMatrix we will optimally exploit every single bit.
	*/
	int sizeOfIntegerColumns,i,j;
	sizeOfIntegerColumns=((g->numberOfVertices)*(g->numberOfVertices))/32+1;
	(g->adjacencyMatrix)=(unsigned int*)malloc(sizeof(unsigned int)*sizeOfIntegerColumns);
	for(i=0;i<sizeOfIntegerColumns;i++)
		(g->adjacencyMatrix)[i]=0;
}
void createEdge(struct Graph*g,int a,int b)
{
	set_two_D_bit_array(a,b,g->adjacencyMatrix,g->numberOfVertices);
}
void removeEdge(struct Graph*g,int a,int b)
{
	reset_two_D_bit_array(a,b,g->adjacencyMatrix,g->numberOfVertices);
}
void showAdjacencyMatrix(struct Graph*g)
{
	int i,j,bitNumber;
	printf("The adjacency Matrix of the Graph is as follows : \n");
	for(i=0;i<(g->numberOfVertices);i++)
	{
		for(j=0;j<(g->numberOfVertices);j++)
			printf("%d",get_two_D_bit_array(i,j,g->adjacencyMatrix,g->numberOfVertices));
		printf("\n");
	}
}
int findNumberOfComponents(struct Graph*g)
{
	/*
		first of all we need to create a copy of the AdjacencyMatrix.
	*/
	unsigned int *adjacencyMatrix_copy,*flag,sizeOfIntegerColumns,i,j,k,components;
	sizeOfIntegerColumns=((g->numberOfVertices)*(g->numberOfVertices))/32+1;
	adjacencyMatrix_copy=(unsigned int*)malloc(sizeof(unsigned int)*sizeOfIntegerColumns);
	for(i=0;i<sizeOfIntegerColumns;i++)
		adjacencyMatrix_copy[i]=(g->adjacencyMatrix)[i];
	/* copy of adjacencyMatrix created */

	/* 	now we need to keep the track of vertices being merged
		for this we need to introduce a one-D bit array that will keep track of this information.
		let this one-D bit array be flag.
	*/
	flag=(unsigned int *)malloc(sizeof(unsigned int)*(g->numberOfVertices)/32+1);
	for(i=0;i<(g->numberOfVertices)/32+1;i++)
		flag[i]=0;
	/*
		if the nth bit of flag array is 0 this means that the vertex with vertexNumber 'n' is still
		alive and is not merged with any other vertex.

		if the nth bit of flag array is 1 this means that the vertex with vertexNumber 'n' is dead
		and is merged with some other vertex and has no existence now.
	*/
	/* now we are ready for merging vertices in our dummy (copied) adjacencyMatrix.  */
	for(i=0;i<(g->numberOfVertices);i++)
	{
		if(get_one_D_bit_array(i,flag)==0) // means ith vertex is alive
		{
			for(j=0;j<(g->numberOfVertices);j++)
			{
				if(j!=i && get_one_D_bit_array(j,flag)==0) // means the jth vertex is alive
				{
					if(get_two_D_bit_array(i,j,adjacencyMatrix_copy,g->numberOfVertices)==1)
					{
						/*
							now we need to merge the ith node with the jth node
							for this we need to merge
								ith row with jth row, and
								ith col with jth col
						*/
						for(k=0;k<(g->numberOfVertices);k++) // merging the ith and jth rows
						{
							if(get_two_D_bit_array(i,k,adjacencyMatrix_copy,g->numberOfVertices) | get_two_D_bit_array(j,k,adjacencyMatrix_copy,g->numberOfVertices))
								set_two_D_bit_array(i,k,adjacencyMatrix_copy,g->numberOfVertices);
						}
						for(k=0;k<(g->numberOfVertices);k++) // merging the ith and jth cols
						{
							if(get_two_D_bit_array(k,i,adjacencyMatrix_copy,g->numberOfVertices) | get_two_D_bit_array(k,j,adjacencyMatrix_copy,g->numberOfVertices))
								set_two_D_bit_array(k,i,adjacencyMatrix_copy,g->numberOfVertices);
						}
						/* now the jth vertex is merged with ith vertex so the ith vertex should have no existence */
						/* so we need to set the jth bit of flag array to 1 */
						set_one_D_bit_array(j,flag); // declaring that the jth vertex is now dead.
					}
				}
			}
		}
	}
	/* 
		now the total number of components in the graph will be the number of vertices that still have zero 
		correponding to their vertex number in flag array.
	*/
	components=0;
	for(i=0;i<(g->numberOfVertices);i++)
		if(get_one_D_bit_array(i,flag)==0)
			components++;
	return components;
}

main.c

#include<stdio.h>
#include"graph.h"

int main()
{
 int i,n,a,b;
 struct Graph*g;
 g=makeNewGraph();
 printf("Enter the number of Vertices in the Graph : ");
 scanf("%d",&(g->numberOfVertices));
 printf("Enter the number of Edges in the Graph : ");
 scanf("%d",&(g->numberOfEdges));
 initializeAdjacencyMatrix(g);
 printf("NOTE : The ordering of the vertices is zero indexed.\n");
 for(i=0;i<(g->numberOfEdges);i++)
 {
  printf("Enter the edge Number %d : ",i+1);
  scanf("%d%d",&a,&b);
  createEdge(g,a,b);
 }
 showAdjacencyMatrix(g);
 printf("Number of components in the Graph = %d\n",findNumberOfComponents(g));
 printf("\nProgram execution successful...\n");
 return 0;
}

Makefile

all: hello
hello: one_D_bit_array.o two_D_bit_array.o graph.o main.o
 gcc one_D_bit_array.o two_D_bit_array.o graph.o main.o -o hello
one_D_bit_array.o: one_D_bit_array.c
 gcc -c one_D_bit_array.c
two_D_bit_array.o: two_D_bit_array.c
 gcc -c two_D_bit_array.c
main.o: main.c
 gcc -c main.c
graph.o: graph.c
 gcc -c graph.c

To find the source code on GitHub click here